DAiR Workshop 2024

Author: Dr. Hamed Abdollahi  
PI: Dr. Homayoun Valafar  

 

Section Goals:

Gain an understanding of the dataset by performing initial exploration and cleaning

Determine if the data follows a normal distribution

Measure the strength and direction of the relationship between two variables.

Determine if there is a significant association between categorical variables (Chi-Square) and if there are differences between groups (T-Test)

Apply appropriate tests based on the data distribution

Reduce the dimensionality of the dataset

Statistical Approach

The three main approaches in statistical modeling:

1. Frequentist

   • Approach to Probability: Uses the frequency or long-run proportion of events to describe probabilities.

   • Often considered more objective, suited for analyzing experiments.

   • Emphasizes rigorous, formal mathematical methods for analyzing and interpreting data.

   • Includes p-values and confidence intervals.

2. Bayesian

   • Bayesian statistics is an approach to data analysis and parameter estimation based on Bayes’ theorem:

     \[ P(A∣B)=P(B∣A)P(A)⋅P(B) \]

     where 𝐴 and 𝐵 are events and 𝑃(𝐵)≠0

   • Allows for the incorporation of prior knowledge and can be updated as new evidence becomes available.

   • More adaptable, suited for situations requiring subjective information or updating predictions with new data.

   • Also emphasizes rigorous mathematical methods, similar to the frequentist.

3. Machine learning:

   • Develops algorithms and computational tools to automatically identify patterns in data and make predictions based on those patterns.

   • Emphasizes practical, data-driven approaches where methods are evaluated based on their predictive performance on test datasets.

   • Less emphasis on theoretical properties compared to statistical inference; focuses more on empirical performance and scalability.

Data vs. Information

• Information: Information is derived knowledge, obtained through various activities like measurement, analysis, observation, etc. One way to communicate and store information is by encoding it.

• Data: Encoded information that is collected, captured, or measured.

  Types of Encoded Information (Data)

  1. Numeric Data:

     • Continuous Data: Can take any value within a range (e.g., temperature).

     • Count (Discrete) Data: Values are restricted to integers (e.g., number of people).

  2. Categorical Data:

     • Ordered (Ordinal) Data: Categorical data with a predefined order (e.g., rating scales).

     • Unordered (Nominal) Data: Categorical data without a specific order (e.g., types of fruits).

     • Binary Data: Categorical data where the only possible values are 0 and 1, where an event is either a “hit” or a “miss”.

  Methods of Data Collection

  1. Observational Data:

     • Collected by passive observation without intervention, based on what is seen or heard.

  2. Experimental Data:

     • Collected following a scientific method with a prescribed methodology, actively and deliberately. Often involves treatment and control groups in studies like clinical drug trials.

  Data Structure

  • Structured Data: Organized in rows and columns, presenting a clear order and format for analysis.

  • Unstructured Data: Lacks a predefined structure and requires techniques to organize and prepare it for analysis.

  Normal Distribution

  • A type of data distribution where:

    • The mean equals the median.

    • Approximately 2/3 (68%) of the data lie within one standard deviation (SD) of the mean.About 95% of the data are within two standard deviations.

    • Roughly 97% of the data are within three standard deviations.

    • At 0, the mean equals the median, indicating a normally distributed data set.

  Skewed Distribution

  • A type of data distribution where the median does not equal the mean.

  • Types:

    • Left-Skewed Distribution: Characterized by a long tail on the left side of the graph.

    • Right-Skewed Distribution: Characterized by a long tail on the right side of the graph.

  

  • The standard normal (z) distribution

    • The pnorm( ) function gives the area, or probability, below a z-value:

    • A two-tailed test is used when you want to test if a sample mean is significantly different from a population mean in both directions.

• The qnorm( ) function gives critical z-valuescorresponding to a given lower-tailed area:

• The t distribution

  • The pt( ) function gives the area, or probability, below a t-value. For example, the area below t=2.50 with 25 d.f. is

  • The qt( ) function gives critical t-values corresponding to a given lower-tailed area:

• The chi-square distribution

  • The pchisq( ) function gives the lower tail area for a chi-square value:

• Multidimensional Data:

  • A multidimensional data set is represented by a \(n \times d\) data matrix, which can also be visualized as a table with n rows and d columns.

  • \(\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n\)​ denote the n rows of the data matrix D.

  • Each \(\mathbf{x}_i\) (where i ranges from 1 to n) represents an individual observation or instance in the dataset.

• Dataset:

  • The simplest form used in statistics and machine learning is tabular data.

  • A structured table of data where:

    • Rows: Each row represents a measured instance of associated information, often referred to as observations, records, tuples, or trials.

    • Columns: Each column lists specific pieces of information (features, fields, attributes, predictors, variables) organized under a common encoding for comparison across instances.

      The data matrix D is structured as follows:

      \[ D = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1d} \\ x_{21} & x_{22} & \cdots & x_{2d} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nd} \end{bmatrix} \]

      Where:

      \(\vec{x}_i = [x_{i1}, x_{i2}, \ldots, x_{id}]\) represents the i-th observation.

• Data Point:

  • The intersection of an observation (row) and a feature (column) in a dataset, \(xij\).

• Robust

  • Refers to an estimate being less susceptible to outliers.

• Regression

  • A method to analyze the impacts of independent variables on a dependent variable.

  • Types

    • ANOVA and models are both types of regression analyses.

• General Linear Model

  • Formulas representing the expected value of a response variable for given values of one or more predictors.

  • Typically represented as y=mx+b.

  • Use lm() to construct these models.

• Generalized Linear Model

  • Models that tweak the normal formula in one way or another to measure outcomes that general linear models can’t address, abbreviated as GLM.

  • Only logistic models will be used.

  • Use glm() to construct these models.

• Kurtosis

  • Measures the size of the tails in a distribution.

Classical Statistics

Classical statistics covers essential topics that are central to data analysis, including:

• Estimation: The process of inferring the value of a population parameter based on a sample.

• Quantification of Uncertainty: Assessing the reliability and variability of estimates and predictions.

• Hypothesis Testing: Evaluating hypotheses about population parameters based on sample data.

These topics form the foundation for analyzing data, making decisions, and drawing conclusions from data.

Estimate

• A statistic calculated from your data.

• Called an estimate because it approximates population-level values from sample data. It’s synonym is “Metric.”

library(palmerpenguins)
data<-penguins

Function	Description
abs(x)	Computes the absolute value |x|.
sqrt(x)	Computes the square root of x.
log(x)	Computes the logarithm of x with the natural number e as the base.
log(x, base = a)	Computes the logarithm of x with the number a as the base.
a^x	Computes a^x.
exp(x)	Computes e^x.
sin(x)	Computes sin(x).
sum(x)	When x is a vector x = (x1, x2, x3, ..., xn), computes the sum of the elements of x: sum(x) = sum(i=1 to n) xi.
prod(x)	When x is a vector x = (x1, x2, x3, ..., xn), computes the product of the elements of x: prod(x) = prod(i=1 to n) xi.
pi	A built-in variable with value π, the ratio of the circumference of a circle to its diameter.
x %% a	Computes x modulo a.
factorial(x)	Computes x!.
choose(n, k)	Computes n choose k (binomial coefficient).

Hypothesis Testing and P-Values

• Statistical hypothesis testing is used to determine which of two complementary hypotheses is true.

• In statistics, a hypothesis is a statement about a parameter in a population, such as the population mean value.

  • Example Structure of a statement:

    “If I [do this to the independent variable], then [this will happen to the dependent variable].”

• The two hypotheses are:

  1- Null Hypothesis (H0): This corresponds to “no effect,” “no difference,” or “no relationship.”

  2- Alternative Hypothesis (H1): This corresponds to “there is an effect,” “there is a difference,” or “there is a relationship.”

• Conducting the Hypothesis Test Formulate the Hypotheses:

  1- Null Hypothesis \((H0): \triangle=0\)

  • The mean weight of apples in a farm is 150 grams.

    • Notation: \(H_0: \mu = 150\)

  2- Alternative Hypothesis \((H1): \triangle ≠ 0\)

  • The mean weight of apples in a farm is not 150 grams.

    • Notation: \(H_a: \mu \neq 150\)

  3- One-way Test (One-tailed Test)

  • A one-way test, or one-tailed test, considers the possibility of an effect in one direction only.

  • This type of test is used when you have a specific direction in which you expect the results to go.

    • Example: Testing if the mean weight of apples is greater than 150 grams.

    • Notation: \(H_a: \mu > 150\)

  4- Two-way Test (Two-tailed Test)

  • A two-way test, or two-tailed test, considers the possibility of an effect in both directions.

  • This test is used when you do not have a specific direction for the effect and want to test for any difference.

    • Example: Testing if the mean weight of apples is different from 150 grams (could be either greater or less).

    • Notation: \(H_a: \mu \neq 150\)

  5- Select the Significance Level \((\alpha)\):

  • Alpha (α) is the probability of rejecting the null hypothesis (H0) when the alternative hypothesis (Ha) is true.
  • Ranges 0 to 1.
  • Common choices for \(\alpha\) are 0.05, 0.01, and 0.10.

  4- Calculate the Test Statistic:

  • Depending on the test, this could be a t-statistic, z-statistic, etc.

  5- Determine the P-Value:

  • The p-value (frequentist statistics) is the probability of obtaining a test statistic at least as extreme as the one observed, assuming that the null hypothesis is true.

    \(\binom{n}{r}=\frac {n!}{r!(n−r)!}​\)

  • If the p-value is less than or equal to the significance level \(\alpha\), we reject the null hypothesis.

• The purpose of hypothesis testing is to determine which of the two hypotheses to believe in.

• The null hypothesis won’t be rejected unless there is compelling evidence against it.

  Types of Errors:

  • Type I Error: Rejecting \(H0\)​ when it is true (false positive). The probability of committing a Type I error is \(\alpha\).

  • Type II Error: Failing to reject \(H0\) when \(H1\)​ is true (false negative).

  • Lower \(\alpha\) reduces the risk of Type I errors but increases the risk of Type II errors.

  • Higher \(\alpha\) increases the risk of Type I errors but decreases the risk of Type II errors.

A common choice is to use \(\alpha = 0.05\) as the cut-off, meaning that the null hypothesis is falsely rejected in 5% of all studies where it is, in fact, true, or that 1 study in 20 finds statistical evidence for alternative hypotheses that are false.

Tests and Models

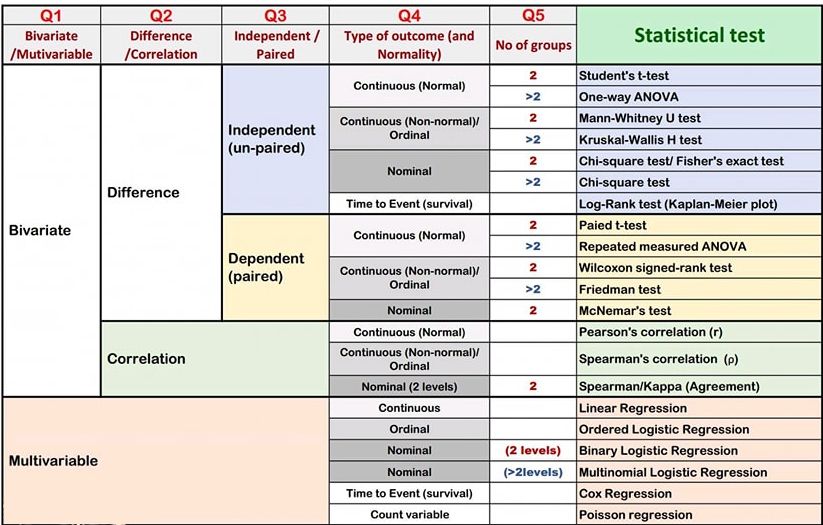
Types of Statistical Tests

1. Parametric: Applicable to normal distributions.

   • Used to compare means of groups.

     • Student’s t-test

     • Paired Student’s t-test

     • Analysis of Variance (ANOVA) Test

     • Repeated Measures ANOVA Test

   • Applied to samples with normally distributed numeric data.

   • Utilize the actual values of the variable.

2. Non-Parametric: Applicable to any distribution.

   • Used to compare medians of groups.

     • Mann-Whitney U Test

     • Wilcoxon Signed-Rank Test

     • Kruskal-Wallis H Test

     • Friedman Test

   • Applied to samples with non-normally distributed numeric data or ordinal data.

   • Utilize the ranks of the values.

Correlation test

• Correlation measures how closely related two variables are. It is suitable to studying the association between two variables.

• A positive value close to 1 indicates a strong positive linear relationship (as one variable increases, the other tends to increase).

• A value close to 0 indicates no linear relationship.

• A negative value close to -1 indicates a strong negative linear relationship (as one variable increases, the other tends to decrease).

  • Pearson’s Test: Assumes data follows a normal distribution and calculates linear correlation.

  • Spearman’s Test: Does not require normality; evaluates non-linear correlation.

  • Kendall’s Test: Also does not require normality; assesses non-linear correlation and is more robust. However, it is more complex to compute manually and is less commonly used.

  • CHi-Square test

    • A statistical test used to determine if there is a relationship between two categorical variables.

    • Null Hypothesis: Assumes that the variables are independent of each other.

  • Comparing Tests: Results from different tests cannot be directly compared; Kendall’s correlation coefficients typically range 20-40% lower than Spearman’s.

Bivariate Analysis

• Involves two variables.

• Aims to determine the relationship or association between the two variables.

  • Independent (Unpaired) Data:

    • Observations in each sample are not related.

    • No relationship exists between the subjects in each sample.

    • Characteristics:

      • Subjects in the first group cannot also be in the second group.

      • No subject in either group can influence subjects in the other group.

      • No group can influence the other group.

    Dependent (Paired) Data:

    • Paired samples include:

      • Pre-test/post-test samples (a variable is measured before and after an intervention).

      • Cross-over trials.

      • Matched samples.

      • When a variable is measured twice or more on the same individual.

Multivariate Analysis

• Involves more than two variables.

• Aims to understand how multiple factors simultaneously impact an outcome.

• Uses regression models to quantify the effect of each variable while controlling for the others.

t-Test

• A statistical method used to compare the means of two groups.

• If your group variable has more than two levels, it’s not appropriate to use a t-test; instead, use an ANOVA (Analysis of Variance).

• Types of t-test

  1. One Sample T-test:

     • Compares the mean of a sample to a known value (population mean).

     • Used when comparing the mean of a sample to a known value (population mean).

  2. Paired T-test (Dependent T-test):

     • Compares the means of two related groups (e.g., before and after treatment).

     • Used when comparing the means of two related groups (e.g., before and after treatment).

  3. Unpaired T-test (Independent T-test):

     • Compares the means of two independent groups.

       • Student’s T-test:

         • Used when the variance in both groups is assumed to be equal.

         • Also known as the Equal Variance T-test or Two Sample T-test.

         • Used when the sample sizes and variances of the two groups are assumed to be equal.

       • Welch T-test:

         • Used when the variance in the two groups is assumed to be unequal.

         • Also known as the Unequal Variance T-test or Welch’s T-test.

         • Used when the sample sizes and variances of the two groups are different.

  Chi-Square test

  • Test of Independence

  • Test of Association

  • It is a non-parametric test used to determine if there is a relationship between two categorical variables.

  • The null hypothesis states that no relationship exists between the variables (they are independent).

  • It compares categorical variables and cannot be used to compare numerical variables.

  • It indicates whether the two variables are dependent or independent but does not specify the type of relationship between them.

  • There must be a Contingency Table which:

    • Has at least two rows and two columns (2x2).

    • Is used to present categorical data in terms of frequency counts.

  • Two Categorical Variables: Each variable should have at least two groups (e.g., Gender with groups Female and Male).

  • Independence of Observations: There should be independence both between and within subjects in the data.

  • Large Sample Size: This ensures the validity of the test results.

    • Expected Frequencies: Each cell in the contingency table should ideally have an expected frequency of at least 1.

    • Majority of Cells: At least 80% of the cells should have expected frequencies of at least 5.

  Correlation test

  • Correlation tests are used to measure the strength and direction of relationships between variables. Here are the key points:

  • Correlation quantifies whether greater values of one variable correspond to greater values of another variable. It is scaled between +1 and -1:

    • Positive Correlation: Values increase together.

    • Negative Correlation: One value decreases as the other increases.

    • Zero Correlation: No apparent link between the values.

    Correlation Methods

    1. Pearson’s Test: Assumes normal distribution and measures linear correlation between continuous variables.

    2. Spearman’s Test: Non-parametric test that does not assume normality; measures non-linear correlation, suitable for continuous or ordinal variables.

    3. Kendall’s Test: Non-parametric test similar to Spearman’s, also measures non-linear correlation but less commonly used.

       Differences Between Pearson’s and Spearman’s Tests

       	Pearson’s Test	Spearman’s Test
       Type	Parametric	Non-parametric
       Relationship	Linear	Non-linear
       Variables	Continuous	Continuous or ordinal
       Sensitivity	Proportional change	Change not at constant rate

    ANOVA

    • ANOVA (Analysis of Variance) is a statistical test used to compare the means of three or more groups of data. Here are the key points:

    • Types of ANOVA

      1. One-way ANOVA

         • Compares the means of three or more groups based on a single independent variable (or factor).

         • Requires at least three observations within each group.

      2. Two-way ANOVA

         • Compares the means of three or more groups considering two independent variables (or factors).

         • Evaluates how each variable individually and together affect the dependent variable.

      Assumptions

      • Independence: Observations within each sample are independent and identically distributed (iid).

      • Normality: Data in each sample follows a normal distribution.

      • Equal Variance: Variances across all samples are equal.

      Interpretation

      • Null Hypothesis (H0): Assumes all group means are equal.

      • Alternative Hypothesis (H1): States that at least one group mean is different from others.

  • After determining that there are differences among the samples, pairwise comparisons must be conducted to identify which specific groups differ from each other.

  • As the number of comparisons increases, the probability of a false positive (Type I error) increases dramatically (e.g., 90% probability with α = 0.05).

  • Post-hoc tests address this issue by adjusting the significance level (α) to maintain an overall desired level of significance across multiple comparisons.

  • Common post-hoc tests include:

    • Tukey HSD: Compares all possible pairs of groups to each other.

    • Dunnett: Compares treatment groups with a control group.

    • Bonferroni Correction: Divides the desired global α level by the number of comparisons (α’ = α / number of comparisons).

  Kruskal-Wallis test

  • The Kruskal-Wallis test is utilized to compare three or more groups based on a quantitative variable, extending the Mann-Whitney test, which compares two groups under non-normality assumptions.

  • Null Hypothesis (H0): The three penguin species have equal bill lengths.

  • Alternative Hypothesis (H1): At least one species differs in bill length from the other two species.

  • It’s important to note that rejecting the null hypothesis does not imply that all species differ in flipper length; it means at least one species differs from the others.

  • The Kruskal-Wallis test requires a quantitative dependent variable (bill length) and a qualitative independent variable (penguin species with at least three levels).

  • It is a nonparametric test, hence it does not assume normality.

  • The observations must be independence groups.

  • Equality of variances is not required for comparing groups but is necessary if comparing medians directly.

  • It’s essential to identify which specific group(s) differ from the others using post-hoc tests, also known as multiple pairwise-comparison tests, which conducted after obtaining significant results from the Kruskal-Wallis test.

  • Common post-hoc tests following a significant Kruskal-Wallis test include:

    • Dunn test

    • Conover test

    • Nemenyi test

    • Pairwise Wilcoxon test